

tems of all options tailored to better prepare you for your tests
Start learningCalculer la puissance 28. La puissance 28 =
a. 16
b. 10
c. 64
d. 128
e. 256
Effectuer l’opération S = 30 + 31 + 32+ 33+ 34. 𝑆 =
a. 121
b. 30
c. 81
d. 31
e. 120
Calculer le nombre 7 en base 2. 7(Base 2) =
a. 100
b. 011
c. 101
d. 111
e. 001
Quel nombre faut-il ajouter à 426 pour avoir 1273 ?
a. 1699
b. 426
c. 847
d. 1273
e. 273
Le nombre 102 est divisible par, à l’exception de :
a. 2
b. 3
c. 7
d. 5
e. 17
L’assertion fausse est :
a. L’entier 1 n’est pas premier
b. L’entier 7 est premier
c. L’entier 3 est un diviseur de 51
d. Le nombre 68 est multiple de 17
Aucune
L’assertion vraie est :
𝑎. −7 > + 1
𝑏. −9 < +9
𝑐. 0 < −3
𝑑. −1 ≠ +1
𝑒. −9 > 0
Mathématique2
Calculer la puissance 28. La puissance 28 =
a. 16
b. 10
c. 64
d. 128
e. 256
Effectuer l’opération S = 30 + 31 + 32 + 33 + 34 .S=
121
30
81
31
120
Calculer le nombre 7 en base 2. 7(Base 2) =
100
011
101
111
001
Quel nombre faut-il ajouter à 426 pour avoir 1273 ?
1699
426
847
1273
273
Le nombre 102 est divisible par, à l’exception de :
2
3
7
5
17
L’assertion fausse est :
L’entier 1 n’est pas premier
L’entier 7 est premier
L’entier 3 est un diviseur de 51
Le nombre 68 est multiple de 17
Aucune
L’assertion vraie est :
−7 > + 1
−9 < +9
0 < −3
−1 ≠ +1
−9 > 0
L’expression (−3) + (−2) − (−7) − (+2) est égale à :
-14
-12
0
4
-10
L’expression (−7)(−3)(+2) − (−5)(−8)(+1) est égale à :
-2
2
1
82
0
L’expression (−7)(−3)(+2) − (−5)(−8)(+1) est égale à :
-2
2
1
82
0
L’expression [(−18) ÷ (+3)] × [(+18) ÷ (−9)] est égale à :
12
-12
-27
27
-18
L’expression (+3)3× (+3)-2+ (+2)2× (−1)7est égale à :
5
7
-1
7
1
Le périmètre d’un rectangle de longueur 3,27 m et de largeur 2,47 m est :
11,48 m
5,74 m
8,0769 m
32,9476m
0,8m
L’expression 0,84 + 2,7 – 3,26 est égale à
3,54
0,28
-0,28
6,8
28
La division du nombre décimal 32,20 par 0,2 donne :
0,161
1,61
2,24
161000
161
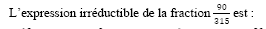
13/63
2/7
6/21
30/105
10/35
Si 2à livres coûtent 60 000 FC, combien coûteront cinq livres ?
300FC
45000FC
10000FC
15000FC
30000FC
La valeur numérique de l’expression algébrique 6𝑥 + 10𝑦 − 4𝑧 pour
𝑥 = −2; 𝑦 = +3 𝑒𝑡 𝑧 = + 5 est :
-2
2
62
32
30
La valeur numérique de l’expression algébrique 4𝑥2+ 4𝑥𝑦 + y2 pour 𝑥 = −1/2𝑒𝑡 𝑦 = 2 est :
9
2
1
8
5
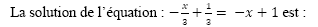
-1
1
2/3
-1/3
-2/3
En utilisant la règle de suppression des parenthèses le calcul de l’expression :
-2(- 5 + 9) – 3(7 -8) + (- 1 +6) donne :
2
-12
- 2
12
0
Le calcul du produit (13,09 × 48,15) diminué de sa moitié donne :
630,2835
315,14175
– 315,14175
30,62
61, 24
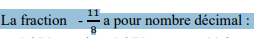
– 1,375
1,375
– 11,8
11,8
- 8,11
Après la réduction du polynôme 16x² + 10x - 12x² - 9x +𝑥 ଷ , sa valeur numérique pour x = - 1 est :
6
-2
2
- 6
0
L’assertion fausse est :
Deux points distincts déterminent une droite
Si deux points d’une droite appartiennent à un plan, alors la droite appartient à ce plan.
Trois points distincts n’appartenant pas à une même droite déterminent un plan
Deux droites sécantes se coupent en un point
Deux droites parallèles sont deux droites coplanaires qui se coupent
L’assertion fausse est :
la mesure de la surface d’un carré est le carré de son côté
la mesure de la surface d’un parallélogramme est le produit de la base et sa hauteur
la mesure de la surface d’un losange est la moitié du produit de la grande diagonale et de la petite diagonale
la mesure de la surface d’un rectangle est le produit de sa longueur et de sa largeur
Aucune bonne assertion
Une pyramide de base b et de hauteur h a pour volume V égal à :
bh
3bh
bh
3
(bh)3
2bh
3