Multiplication, division et propriétés dans N

Exemple de situation

L’enseignant de 7^e année de l’EB du collège ELIKYA à Kinshasa a un pigeonnier composé de 240 pigeons. Chaque femelle pond 2 œufs.

L’enseignant est très content car 160 femelles ont pondu des œufs, mais a de l’inquiétude pour celles qui n’ont pas pondu.

En classe, il demande à ses élèves de trouver le nombre de pigeonneaux de 160 femelles et de déduire le nombre de femelles de 160 pigeonneaux qu’il désire avoir prochainement.

Rappel

• Effectuez les opérations suivantes dans N :

1. a) 144+66
2. b) 333+93
3. c) 58+625

• Effectuez les opérations suivantes :

1. a) 526×17
2. b) 526×0
3. c) 1 × 37
4. d) 105 : 7
5. e) 81 : 27

Motivation

Amener la classe à faire une lecture individuelle en silence, ensuite à haute voix par 2 ou 3 élèves.

Expliquer la situation avec ses propres mots.

Analyse 

Par groupe de deux élèves :

• Identifier les objets
• Identifier les actions à mener pour la situation

Par groupe de deux élèves :

• Identification des entiers naturels 
• Action à mener :

• Restituer la définition du produit et du quotient de deux nombres
• Restituer les propriétés de la multiplication et de la division dans N
• Expliquer la disposition pratique pour multiplier ou diviser 2 nombres

Disposition pratique

Exemple : 540 : 45

Propriétés de la division dans N

 situation

L’enseignant de 7^e année de l’EB du collège ELIKYA à Kinshasa a un pigeonnier composé de 240 pigeons. Chaque femelle pond 2 œufs.

L’enseignant est très content car 160 femelles ont pondu des œufs, mais a de l’inquiétude pour celles qui n’ont pas pondu.

En classe, il demande à ses élèves de trouver le nombre de pigeonneaux de 160 femelles et de déduire le nombre de femelles de 160 pigeonneaux qu’il désire avoir prochainement.

• Effectuez les opérations suivantes dans N :

1. a) 144+66   =  210
2. b) 333+93   =  240
3. c) 58+625   =  Impossible (car 58<625)

• Effectuez les opérations suivantes :

1. a) 526×17  =  19462
2. b) 526×0    =   0
3. c) 1 × 37     =  37
4. d) 105 : 7    =  15
5. e) 81 : 27    =   3

Compréhension de la situation

Les élèves font la lecture en silence, puis à haute voix.

Explication de la situation en restituant la règle de calcul pour multiplier 2 entiers naturels, pour diviser 2 entiers naturels.

• Restituer la définition du produit et du quotient de deux nombres naturels.
• Expliquer la disposition pratique pour multiplier 2 nombres
• Enoncer la formule générale de la division
• Diviser 540 par 45 en disposant pratiquement.
• Citer les propriétés de la multiplication et de la division dans N

Participation des élèves à la production de la synthèse

1. Le produit de deux naturels a et b est la somme de a nombre naturels égaux à b.

On le note : a × b ou a .b

(a et b sont appelés facteurs)

Exemple : 3 ×5=5+5+5 =15

. 7 × 6 = 6+6+6+6+6+6+6 = 42

Propriétés. 3 × b = b +b+ b = 3 b 

• La multiplication dans N est :

• Commutative : a × b = b × a

         Exemple : 2 × 3 = 3×2

• Associative : (a ×b) ×c=a× (b ×c)
• Elément neutre de la multiplication a×1=1×a=a
• Elément absorbant : a×0=0×a=0
• Stable : a ×b ϵ N
• Distributivité de la multiplication à l’addition et à la soustraction :

• a × (b +c) = (a ×b) + (a ×c)
• a × (b-c) = (a ×b)-(a ×c)

Ceci est appelé développement.

• Dans la disposition pratique pour multiplier, il est conseillé de choisir pour multiplicateur le facteur qui comprend le moins des chiffres significatifs différents.

Exemple : Entre 15037 et 1234 choisir 15037

2. Le quotient de 2 naturels a et b est le rapport de a et b, avec b≠0

* Formule générale : D=d .q +r(r<d)

- La division est exacte si r=o, au cas contraire il est avec reste.

pratique

Exemple : 540 : 45

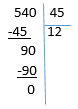
Propriétés de la division dans N

Si on multiplie (divise) le dividende et le diviseur par un même nombre non nul, le quotient ne change pas mais le reste est multiplié (divisé) par ce même nombre. Le reste ainsi obtenu est appelé valeur relative du reste.

Exemple : 

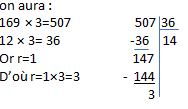
N.B : Aucun nombre n’est divisible par 0.