

Rappel
Définir en extension
a) {x ∊ IN : x = 3y, y ∊ IN, 3 ≤ y < 7}
b) {x ∊ ∣ x ∣ ; 4x + 1 ≤ 7}
Motivation
Considérons les ensembles
A = {1,2,3,4} et B = {0,1,2,3,4,5}
Que constatons-nous de ces deux ensembles ?
Que pouvons-nous dire de A par rapport à B ?
Annonce du sujet
Aujourd'hui, nous allons étudier
Analyse
Qu'appelle-t-on inclusion de deux ensembles ?
Qu'est-ce que l'inclusion de deux ensembles A et B ?
a) {x ∊ IN : x = 3y, y ∊ IN, 3 ≤ y < 7}
b) {x ∊ ∣ x ∣ ; 4x + 1 ≤ 7}
Définir en extension
3; 4; 5 ⟹ x = 3.3 = 9
x = 3.4 = 12
x = 3.5 = 15
a) A = {9; 12; 15}
b) B = { 0,1 }
A = {1,2,3,4} ; B = {0,1,2,3,4,5}
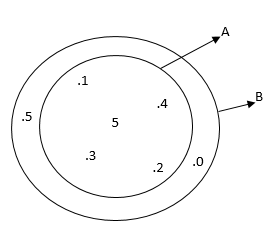
Nous constatons que tout élément de A est aussi élément de B. A est un sous-ensemble de B.
Aujourd'hui, nous allons étudier l'inclusion des ensembles.
Définition
Soit A et B deux ensembles
A est un sous-ensemble de B si tous les éléments de A sont aussi éléments de B.
On écrit : A ⊂ B
On lit : E est inclus dans F ou
E est un sous-ensemble de F ou
E est une partie de F
E est contenue dans F
( E ⊂ F ) ⇔ (∀x,x ∊ E ⟹ x ∊ F)
⊂ : est le symbole d'inclusion
Représentation

N.B: A n'est pas un sous-ensemble de B ssi il existe au moins un élément de A qui n'est pas élément de B. et on écrit A ⊄ B.
- E ⊂ F s'écrit encore F ⊃ E et se lit F contient E
E ⊄ F s'écrit encore F ⊅ E et se lit F ne contient pas E
Un ensemble A est inclus dans un ensemble B si tout élément de A et aussi élément de B.