

Rappel
Effectuez ces opérations :
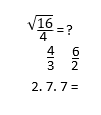
Motivation
Qu'appelle-t-on cette écriture a x2 + a x6 + 7 y3 ?
Annonce du Sujet
Qu'allons-nous étudier aujourd'hui ?
Analyse
Prenons quelques exemples
Un polynôme est une somme algébrique de plusieurs monômes.
Exemple
3 a2 b + 5 ab2 + ab2 + 5
3 x2 + 2 x + 1 + x
Calculez la valeur absolue numérique de :
P (x) = x3 - x2 - 7 x
Pour x = 3
2 a + 3 b - x pour a = -2 b = 4 x = 3
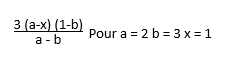
Effectuez ces opérations :


Cette écriture a x2 + a x6 + 7 y3 s'appelle un polynôme.
Aujourd'hui nous allons étudier la somme et produit de deux polynômes.
Un polynôme est une somme algébrique de plusieurs monômes.
Exemple
3 a2 b + 5 ab2 + ab2 + 5
3 x2 + 2 x + 1 + x
Somme et produit de deux polynômes
Réduire les polynômes suivants :
8a - 5b + 3c + 7b - 2a - c+4 =
8a -2a -5b + 7b + 3c - c+4 = 6a + 2b
2c +4
12a -4 -a + 6 -6a - 2 =
a + 4
2 a b x (-3 a b2) = - 6 a2 b3
5 a2 b x3 x 2 a b4 x5 = 10a3 b5 x8
-5 x (- 3 x) x 4 y = 60 xy
3 x 2 a = 6 a
Transformation
3 (a + 2b) = 3a + 6b
- 2a (3 a2 - 5b) = - 6a3 + 10 ab
5 a2 b (-3a3 b2 + 6 a4 - 2 b3) = - 15 a5 b3
+ 30 a6 b - 10 a2 b4
Développement
(3a -2) (-5a-4) = 15 a2 - 12 a + 10 a + 8
→ 15 a2 - 2a +8
(-5x+2y) (-3a -6b x+7)
Mise en évidence
3a+3b = 3 (a+b)
24 a2 + 30 a3 = 6 a2 (4 +5 a)
15 a2 b3 x4 - 30 a2 b4 x + 10 a2 b3 =
5 a2 b3 (3x4 - 6 b x + 2)
Valeur numérique est le nombre obtenu en remplaçant les lettres (variables) par des nombres.
Calculez la valeur absolue numérique de :
P (x) = x3 - x2 - 7 x
Pour x = 3
2 a + 3 b - x pour a = -2 b = 4 x = 3
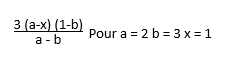
P (3) = 33 - 32 - 7.3
= 27 - 9 - 21 = -23
2(-2) + 3 (4) -3 = - 4 + 12 -3
= -7 + 12 = +5
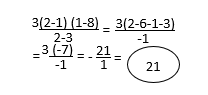
Identités remarquables
Les plus usuelles sont :
Le carré d'une somme;
Le carré d'une différence;
Le cube d'une somme;
Le cube d'une différence.
Le carré d'une somme (a+b)2
(a+b)2 = (a+b) (a+b)
= a2 + ab + ab + b2 = a2 + 2 ab + b2
(2+x)2 = (2+x) (2+x)
4 + 2 x + 2 x + x2
4 + 4 x + x2
(y + 2x)2 = y2 + 4 x y + 4 x2
Au contraire si on a : (a + b + c)2
(a + b + c) (a + b + c) = a2 + b + c2 + 2 a b + 2 b c + a c.
Comment l'effectuer (x + t + 2)2
x2 + t2 + 4 + 2 t x + 4 t + 4 x.
Effectuez (2 a + 2 b)2
4 a2 + 8 a b + 4 b2