

Rappel
Calculer :
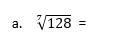
Motivation
Une composition telle que :
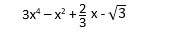 S'appelle...?
S'appelle...?
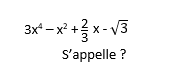
Annonce du Sujet
Analyse
Définir une application polynôme.
Comment peut-on expliquer un polynôme réduit par rapport au polynôme réduit ordonné?
Quand peut-on parler des polynômes constants et égaux?
Qu'est-ce que nous venons de voir?
Calculer :


Une composition telle que :
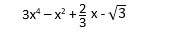
S'appelle polynôme.
Aujourd'hui nous allons étudier les notions des polynômes dans R .
Définition
Une application polynôme se note p(x) = an xn + a n-1 x n-1+... +a 1 x+a0

Un polynôme réduit est ordonné si ses termes sont écrits dans l'ordre des puissances croissantes ou décroissantes de la variable.
h(x) = - 2 x2+ 5x - 1 + 6x + 9x2 + 7x + 14 + 3x4
Réduisons et ordonnons h(x) 3x4 + 7x2 + 18 x + 13
d = 4.
Polynôme constant
Si f(x) = a est un polynôme constant.
Polynômes égaux
Deux polynômes sont égaux ssi les coefficients des monômes de même degré sont égaux.
Valeur numérique d'un polynôme
f(x) = 2x3- 3x2 - 5x +6
f(0) = 2 x 03 - 3 x 02 -5 x 0 +6 = + 6
f(3)= 2 x 33 - 3 x 32 -5 x 3 +6
= 2 x 27 - 3 x 9 - 15 +6
= 54 -27-9 = +18
f(-1) = 2 x(-1)3 - 3 x (-1)2 -5 x (-1)+6
= 2 x (-1) - 3 x 1 - 5 x(-1) +6
= -2-3+5+6 = +6
Nous venons de voir les polynômes dans R : notions.