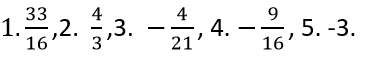5. Dans R2, on définit deux opération * et T respectivement par :
(x,y)*(x’,y’)= (x+x’, y.y’) et (x,y) T(x’,y’)=(x-x’,y/y’ ).
Le couple (x,y) tel que : (x,y)*(-3,y)=(-3,y) T(2,x)
(x,y) vaut :
1.(-2,0), 2.(-1, ½ ), 3. (0, ½ ), 4. ( ½ ,0), 5.(2,0).
6.Dans l’ensemle C= R\{-2} est définit la loi interne « T » par : x T y = xy +2 (x+y+1), où x et y sont des éléments de E, e est l’élément neutre de E, x’ est l’élément symétrique (le symétrique de – ½ ) et x’’ est le symétrique de 2 le rapport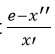 
vaut :
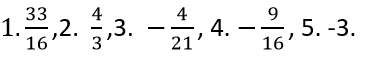
5. Dans R2, on définit deux opération * et T respectivement par :
(x,y)*(x’,y’)= (x+x’, y.y’) et (x,y) T(x’,y’)=(x-x’,y/y’ ).
Le couple (x,y) tel que : (x,y)*(-3,y)=(-3,y) T(2,x)
(x,y) vaut :
1.(-2,0), 2.(-1, ½ ), 3. (0, ½ ), 4. ( ½ ,0), 5.(2,0).
6.Dans l’ensemble C= R\{-2} est définit la loi interne « T » par : x T y = xy +2 (x+y+1), où x et y sont des éléments de E, e est l’élément neutre de E, x’ est l’élément symétrique (le symétrique de – ½ ) et x’’ est le symétrique de 2 le rapport 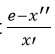vaut :
