

Rappel
Résoudre cette équation :
x2 - 5 x + 6 = 0
Motivation
Comment pouvons-nous appeler a x4 + b x2 + C = 0 avec a ǂ 0 ?
Annonce du Sujet
Aujourd'hui nous allons étudier l'équation bicarrée.
Analyse
Prenons un exemple
x4 - 5 x2 + 6 = 0
Généralisations
Equations trinômes
Qu'est-ce que nous venons de voir?
Résoudre cette équation :

a x4 + b x2 + C = 0 avec a ǂ 0. C'est une équation bicarrée.
Aujourd'hui nous allons étudier l'équation bicarrée.
On appelle équation bicarrée d'indice x, toute équation de la forme a x4 + b x2 + C = 0 avec a ǂ 0
Résolution
Pour résoudre une équation bicarrée, on pose x2 = t , on obtient a t2 + b t + C = 0, à toute racine positive t0 de l'équation correspondent à deux racines réelles opposées x1 et x2
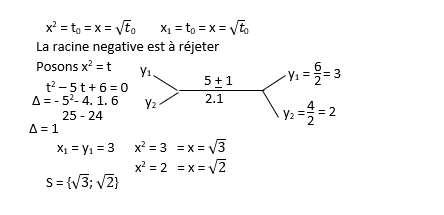
Généralisations
Equations trinômes
a x2n + b xn + C = 0
Avec n Є N* | {1}
x6 - 28 x3 + 27 = 0
x2 - 28 x + 27 = 0
t2 - 28 t + 27 = 0
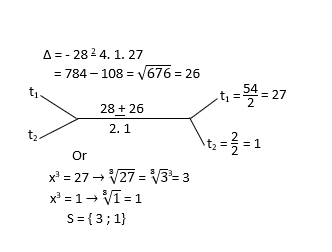
Nous venons de voir les équations bicarrées.