

7. Sont définit dans Q, deux lois de composition interne << *>> et << ⊥>> par: x*y=x+y -xy. et x⊥ y = x+y-1, qui font de (Q , * , ⊥ ) un corps. m et n sont les symétriques de l'élément 1/2 respectivement pour les lois * et ⊥.
l'expression (m+n) vaut:
1. 1/2, 2. 3/2, 3. 5/2, 4. 17/6, 5. 7/2.
8. Dans R, l'opération * est définit par: a*b 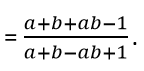 n et y désignent respectivement l'élément neutre et l'élément idempotent. la somme x +y vaut:
n et y désignent respectivement l'élément neutre et l'élément idempotent. la somme x +y vaut:
1. -2, 2.-1, 3.0, 4.1, 5. 2
7. Sont définit dans Q, deux lois de composition interne << *>> et << ⊥>> par: x*y=x+y -xy. et x⊥ y = x+y-1, qui font de (Q , * , ⊥ ) un corps. m et n sont les symétriques de l'élément 1/2 respectivement pour les lois * et ⊥.
l'expression (m+n) vaut:
1. 1/2, 2. 3/2, 3. 5/2, 4. 17/6, 5. 7/2.
8. Dans R, l'opération * est définit par: a*b 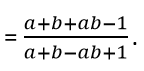 n et y désignent respectivement l'élément neutre et l'élément idempotent. la somme x +y vaut:
n et y désignent respectivement l'élément neutre et l'élément idempotent. la somme x +y vaut:
1. -2, 2.-1, 3.0, 4.1, 5. 2