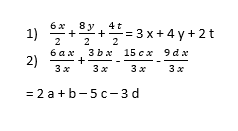Rappel
Déterminez le degré des polynômes par rapport à a, b et x.
Motivation
Quelle est l'opération qui consiste à x5. x6 = ?
Annonce du Sujet
Qu'allons-nous étudier aujourd'hui ?
Analyse
Comment peut-on multiplier les polynômes ?
Comment peut-on diviser un monôme par un monôme ?
On donne A = x + y - 2
B = - 2 x - y + 1
C = x - 2 y - 3
Calculer :
A . B
B . C
A . C
Comment peut-on diviser un polynôme par un monôme ?
Déterminer le degré des polynômes par rapport à a, b et x.
4ème degré par rapport à a ;
5ème degré par rapport à b ;
2ème degré par rapport à x.
L'opération qui consiste à x5. x6 , c'est la multiplication.
Aujourd'hui, nous allons étudier la multiplication et la division de polynômes.
Multiplication d'un polynôme
3 a b (2 a2 b3- 4 a3 + 5 a b2) = 3 a b. 2 a2 b5
= 6 a3 b4 - 12 a4 b + 15 a2 b3
-9 x2 y ( - 3 x2 + 2 y2- x4 y ) =
27 x4 y - 18 x2 + y3 + 9 x6 y2
( - 2 a3 b2 + 3 a2 ) ( a4 b3 + 4 b3- 5 )
- 2 a7 b5 - 6 a3 b5 + 10 a3 b2 + 3 a6 b3 + 12 a2 b3- 15 a2
Division d'un polynôme par un polynôme
Division d'un monôme par un monôme
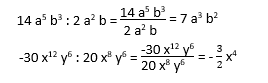
Division d'un polynôme par un monôme

On donne A = x + y - 2
B = - 2 x - y + 1
C = x - 2 y - 3
Calculer :
A . B
B . C
A . C
A .B = (x + y - 2) ( - 2 x - y + 1 )
= - 2 x2 - x y + x - 2 x y - y2 + y
= - 2 x2 - 3 x y + 5 x 3 y - 2
Diviser :
1) 6 x + 8 y + 4 t par 2
2) 6 a x + 3 b x - 15 c x - 9 d x par 3 x