

Rappel
Divisez :
12 a2 b3 - 20 a3 b4 + 16 a5 b2 : 4 a b2
Motivation
Comment s'appelle un procédé qui consiste à mettre une somme des termes en un produit de facteurs ?
Annonce du Sujet
Qu'allons-nous étudier aujourd'hui ?
Analyse
Comment peut-on réaliser la factorisation ?
Quand y a-t-il mise en évidence ?
Comment peut-on employer les identités remarquables ?
Qu'est-ce que nous venons de voir ?
Divisez :
12 a2 b3 - 20 a3 b4 + 16 a5 b2 : 4 a b2.

Un procédé qui consiste à mettre une somme des termes en un produit de facteurs s'appelle la factorisation.
Aujourd'hui, nous allons étudier la factorisation et produits, identités remarquables.
Pour réaliser la factorisation en facteurs, on utilise les méthodes de décomposition telles que :
La mise en évidence
Il y a mise en évidence lorsque tous les termes d'une expression algébrique renferment un facteur commun.
20 a2 x4 - 16 a2 x2 - 24 a3 x = 4 a2 x (5 x3 - 4 x + 6 a)
132 x + 360 y - 84 = 12 (11 x + 30 y - 7)
15 a2 x3 y4 + 5 a4 x5 y6 - 5 a x2 y3 = 5 x2 y3 (3 a x y + a3 x3 y3-1)
Emploi des identités remarquables
Différence de deux carrées
(a-b) (a + b) = a2 + ab - ab - b2
Trinôme carré parfait
( a + b )2 = a2 + 2 a b + b2 (a - b)2 = ?
( 3 x + 2 )2 = ( 3 x + 2 ) ( 3 x + 2 )
= 9 x2 + 6 x + 6 x + 4
9 x2 + 12 x + 4
Quadrinôme cube parfait
( a + b )3 = a3 + 3 a2 b + 3 a b2 + b3
(a - b)3 = a3- 3 a2 b + 3 a b2- b3
(2 x - y2)3 = 8 x3 - 12 x2 y2 + 6 x y4 - y6
( x + 1)3 = x3 + 3 x + 1 + 3 x3
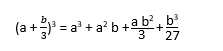
Somme et différence de deux cubes
a3 + b3 = (a + b) (a2- a b + b2)
a3- b3 = (a - b) (a2 + a b + b2)
Trinôme du second degré
Un trinôme du second degré en x est tout trinôme de la forme a x2 + b x + c (1)
( a ǂ 0 )
Nous venons de voir la factorisation et la mise en évidence.