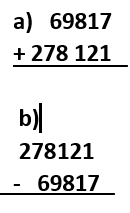Exemple de situation:
Un terrain de tennis du Lycée de Kisantu a la forme d'un rectangle (L=24,53m, l=12,36m).
a) On augmente sa longueur de 3,27m et on diminue sa largueur de 2,47m Calculer le périmètre du nouveau rectangle et le comparer au premier rectangle.
b) On diminue la longueur du premier rectangle de 1,86m et on augmente sa largueur de 0,43m. Comparer le périmètre de ce nouveau rectangle à celui du premier.
1. Calculer:
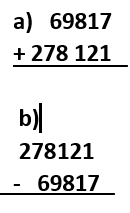
2.. Ecrire et lire trois exemples de nombres décimaux au T.N.
3. De combien de parties est composé un nombre décimal? Citer-les et donner un exemple.
4. Calculer le périmètre d'un rectangle de L=3,97cm et l=2,63cm
2. Motivation
Demander aux élèves de:
- Lire la situation en silence, ensuite à haute voix par deux élèves choisis.
- Expliquer la situation en ses propres termes.
ORGANISATION DE LA CLASSE ET CONSIGNE
- Demander aux élèves de se grouper à cinq ou six.
Consigne:
- Déterminer les objets et les actions à mener pour comparer les périmètres de différents rectangles.
- Traiter la situation
QUESTIONS de récapitulation:
- Présenter la disposition pratique de ces deux opérations?
- Citer les propriétés de l'addition et de la soustraction dans D.
Vérification des acquis
Items: - Calculer:
a) 27,036+304,89+7329,1
b) 467,364-58,289
c) 0,04 + 12,7-3,126
a) 347 938 b) 278 121
2. Réponses proposées individuellement par les élèves.
3) Item
4) Périmètre du rectangle est de 13,2cm.
- Lecture de la situation en silence et à haute voix par un ou deux élèves désignés.
- Explications données par un ou deux élèves et adoptées par toute la classe.
Identification des objets: nombres décimaux
Actions à mener:
- restitution de la définition de l'addition et de la soustraction des décimaux;
- détermination des propriétés de l'addition des décimaux.
- Explication et utilisation de la disposition pratique dans l'addition et la soustraction des nombres décimaux.
- Calcul des périmètres des rectangles après modifications des dimensions.
- Comparaison des périmètres obtenus. (P1=83,78m; P2=77,38m; P3=70,92m. P3≤P2≤P1
SYNTHESE:
Pour avoir la somme ou la différence de deux décimaux:
- on écrit tous les chiffres de même rang sur la même colonne
- ensuite, on calcule comme pour les nombres entiers
- et on place la virgule au résultat sur la colonne des virgules.
- l'addition des décimaux est commutative et associative.
- la soustraction des décimaux n'est ni commutative ni associative.