Factorisation des produits remarquables (MM 1.38)

I. ACTIVITES INITIALES

1. Vérification des connaissances précédentes :

a) Développer ;

(a ± b)² =

b) Factoriser :

a² - b² =

c) Factoriser :

2ax + ay + 2bx + by =

Motivation (découverte)

Demander aux élèves de :

- Lire la situation en silence, ensuite à haute voix par deux élèves choisis.

- Expliquer la situation en leurs propres termes.

II. ACTIVITES PRINCIPALES

Organisation de la classe et consignes

- Regrouper la classe en binômes.

Consignes : identifier :

a) les objets essentiels de la situation

b) les actions à mener.

III. SYNTHESE

Questions de récapitulation

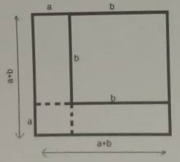
Représenter géométriquement l'aire d'un carré de côté (a + b)

IV. EVALUATION

Vérification des acquis

Géométriquement, que représentent les expressions littérales ab et a² ?

Vérification du traitement de la situation :

Compléter la figure de la situation pour montrer : (a + b)² = a² + 2ab + b².

I. ACTIVITES INITIALES

Réponses aux questions

a) a² ± 2ab + b²

b) (a + b)(a - b)

c) (a + b)(2x + y)

2. Compréhension de la situation

- Lecture de la situation.

• En silence (tout le monde)
• A haute voix par un ou deux élèves désignés

- Explications données par un ou deux élèves et adoptées par la classe (même compréhension).

II. ACTIVITES PRINCIPALES

Activités sur le tableau de spécification

a) Objets : nombres et expressions littérales

2) Actions à mener :

- Restitution de la définition d'un carré et de la formule de l'aire d'un carré;

- Explication géométrique de la représentation du carré d'un nombre;

- Représentation de l'aire d'un carré de côté x + y;

- Développement de l'aire (x + y)² dans une figure;

- Développement de (x + y)² pour calculer les produits remarquables (x + y)²; (x + y)(x-y).

III. SYNTHESE

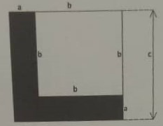
Participation des élèves à la construction de la synthèse :

IV. EVALUATION

Réponses aux questions (items)

a) Ab est le produit d'un rectangle des côtés a et b; et a²; l'aire d'un carré de côté a.

Traitement de la situation