

Exemple de la situation
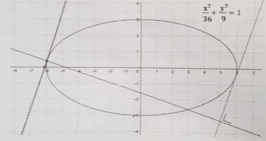
Le menuisier du quartier Kimpe dans la commune de Ngaliema à Kinshasa/Delvaux a réalisé un plan de la table de travail pour internautes en forme ovale à fabriquer (voir figure ci-dessous). Le contour de la table se présente comme une ellipse d'équation :
x2 / 36 + y2/9 = 1.
Il souhaite tracer des tangentes en des points bien choisis et de perpendiculaires en ces points qui représenteront les pieds de la table en vue de séparer les places réservées aux internautes.
Aide-le à :
a) Ecrire l'équation de la tangente (t) au point C(x0, y0) de l'ellipse (E).
b) Ecrire l'équation de la perpendiculaire à la tangente (t) au point C(x0, y0) de l'ellipse (E) et la caractériser.
c) Appliquer les questions a) et b) à l'équation représentant la table de travail fabriqué au quartier Kimpe aux points d'abscisse 2.
ACTIVITES PRINCIPALES
- Repartir les élèves en petits groupes.
(1) Tangente et normale en un point d'une conique
-Restituer : la définition de la tangente à une courbe; la définition de la normale en un point d'une courbe.
- Ecrire : l'équation de la tangente en un point de la courbe; l'équation de la normale à la conique.
(2) Tangentes à une conique issues d'un point.
- Ecrire : l'équation d'une droite (t) passant par le point A donné extérieur à la conique et de coefficient angulaire m à déterminer.
- Résoudre : le système formé par l'équation de la droite (t) et l'équation de la conique donnée.
- Exprimer : la condition de tangence de la droite (t) à la conique donnée.
- Résoudre : l'équation en m résultant de la condition de tangence de la droite (t) à la conique donnée.
- Ecrire : les équations des tangentes cherchées en exprimant que ce sont des droites passant par le point A et de coefficient angulaire m trouvé.
(3) Normales issues d'un point à une conique
- Restituer : l'équation de la << conique d'Apollonius >>
- Déterminer : les pieds de contact des normales en résolvant le système formé par l'hyperbole d'Apollonius et la conique donnée
- Ecrire : les équations des normales issues du point donné et passant par chacun des pieds des normales trouvés.
Exemple de la situation
Le menuisier du quartier Kimpe dans la commune de Ngaliema à Kinshasa/Delvaux a réalisé un plan de la table de travail pour internautes en forme ovale à fabriquer (voir figure ci-dessous). Le contour de la table se présente comme une ellipse d'équation :
x2 / 36 + y2/9 = 1.
Il souhaite tracer des tangentes en des points bien choisis et de perpendiculaires en ces points qui représenteront les pieds de la table en vue de séparer les places réservées aux internautes.

Aide-le à :
a) Ecrire l'équation de la tangente (t) au point C(x0, y0) de l'ellipse (E).
b) Ecrire l'équation de la perpendiculaire à la tangente (t) au point C(x0, y0) de l'ellipse (E) et la caractériser.
c) Appliquer les questions a) et b) à l'équation représentant la table de travail fabriqué au quartier Kimpe aux points d'abscisse 2.
ACTIVITES PRINCIPALES
- Repartir les élèves en petits groupes.
(1) Tangente et normale en un point d'une conique
-Restituer : la définition de la tangente à une courbe; la définition de la normale en un point d'une courbe.
- Ecrire : l'équation de la tangente en un point de la courbe; l'équation de la normale à la conique.
(2) Tangentes à une conique issues d'un point.
- Ecrire : l'équation d'une droite (t) passant par le point A donné extérieur à la conique et de coefficient angulaire m à déterminer.
- Résoudre : le système formé par l'équation de la droite (t) et l'équation de la conique donnée.
- Exprimer : la condition de tangence de la droite (t) à la conique donnée.
- Résoudre : l'équation en m résultant de la condition de tangence de la droite (t) à la conique donnée.
- Ecrire : les équations des tangentes cherchées en exprimant que ce sont des droites passant par le point A et de coefficient angulaire m trouvé.
(3) Normales issues d'un point à une conique
- Restituer : l'équation de la << conique d'Apollonius >>
- Déterminer : les pieds de contact des normales en résolvant le système formé par l'hyperbole d'Apollonius et la conique donnée
- Ecrire : les équations des normales issues du point donné et passant par chacun des pieds des normales trouvés.