

Q4. Effectuer les opérations: le produit, le quotient, la puissance nième et la racine nième de nombre complexe non nul en utilisant la forme trigonométrie d'un nombre complexe.
B. Quotient de deux nombres complexes non nuls.
Soit z1 et z2 deux nombres complexes écrits sous la forme trigonométrique. Calculons leur quotient :
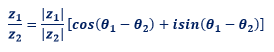
C. Puissance d’un nombre complexe et formule de MOIVRE.
Soit un nombre complexe donné sous la forme trigonométrique :
z=|z|(cosθ + isinθ) (1)
Calculons Zn avec n ∈ N*. On a deux possibilités :
Arg z=n.θ
zn=|z|n(cosnθ + isinnθ) (2)
2. En élevant chaque membre de (1) à la puissance ne, on obtient :
zn=|z|n(cosθ + isinθ)n (3)
Les égalités (2) et (3) impliquent :
(cosθ + isinθ)n = cosnθ + isinnθ
C’est la formule de MOIVRE. Elle permet de calculer la ne puissance d’un nombre complexe non nul.
d. Racine ne d’un nombre complexe non nul.
Tout nombre complexe non nul possède n racines nième distinctes, de même module 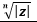 et d’arguments différents de 2kπ/n (k=1,2,3,…,n-1).
et d’arguments différents de 2kπ/n (k=1,2,3,…,n-1).
On obtient ces racines nièmes par la formule suivante :
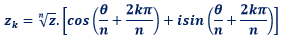
e. Applications de la formule de MOIVRE.
Soit un nombre complexe un nombre complexe zn=(cos x + i sin x)n (1)
zn=u + i v avec u=R(zn) et v=I(zn).
Les égalités (2) et (3) permettent d’écrire :
cos nx = u et sin nx = v qui expriment cos nx et sin nx en fonction de cos x ou sin x.