Représentation des nombres complexes (suite 2)

4.  Effectuer les opérations: le produit, le quotient, la puissance nième et la racine nième de nombre complexe non nul en utilisant la forme trigonométrie d'un nombre complexe. 

1. Linéarisation.

• On appelle linéarisation, la transformation d’un polynôme en cos x ou sin x en une somme de cosinus ou sinus de multiples de x.
• Procédé :

1. Partir des égalités : 

z=cos x + i sin x ou e^ix= i sin x  (1)

z=cos x - i sin x ou e^-ix=cos x-i sin x  (2)

2. Additionner membre à membre les égalités pour obtenir :

3. Soustraire membre à membre (2) et (1) pour obtenir :

Ces formules sont dites d’Euler.

• Elever à la puissance n^ième chaque membre de (1) et (2) en utilisant éventuellement la formule de Moivre pour obtenir :

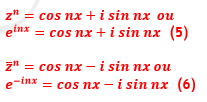
De même, élever à la n^ième puissance chaque membre de (3) et (4) pour obtenir :

• Additionner membre à membre les égalités (5) et (6) pour obtenir :

​​​​​​​

• Soustraire membre à membre les égalités (6) et (5) pour obtenir :

​​​​​​​

• Développer le second membre de (7) et (8) en utilisant le binôme de Newton.

Tenir compte des égalités (9) et (10).

Le résultant qu’on obtient exprime cosⁿ x ou sin^{​​​​​​​n} x comme une combinaison linéaire de cos kx ou sin kx avec 0<k<n.