

Exemple de situation :
Pendant leur leçon de mathématiques, les élèves de 4ème année des HSC de l’Institut 1 BUTA dans le Bas-Uélé ont reçu, parmi les exercices à résoudre en prérequis, l’équation du deuxième degré suivant : x2+2x+2=0.
Tous les élèves sont parvenus à conclure que les solutions de cette équation n’existent pas dans R parce que le discriminant est un nombre négatif. L’enseignant leur demande de : a) Poursuivre la recherche des racines de ces équations en posant, dans le discriminant, i2= -1 ; b) Trouver d’autres équations de ce type ; c) Dire si ces racines sont des nombres réels. Justifier la réponse.
Résoudre dans R les équations suivantes :
L’enseignant demande aux élèves de (d’) :
Organisation de la classe et consigne
Dégager les parties réelle et imaginaire des racines écrites sous forme Z=a + bi, a et b étant des réels
Calculons le discriminant ou réalisant de l’équation :
Δ=b24ac
Δ=72-4.6.(-3)=121>0
L’équation admet deux racines réelles distinctes
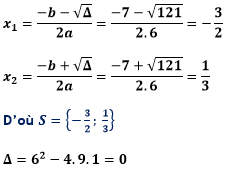
L’équation admet une racine double.
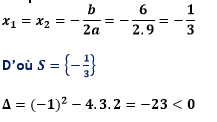
Activités sur le tableau de spécification
L’équation n’a pas de solution dans R.
Trois cas sont possibles :
1er cas : Δ>0, l’équation admet deux racines réelles distinctes x1 et x2 et S= {x1, x2. } Le trinôme ax2+ bx + c se factorise en a(x - x1)(x-x2).
2ème cas : Δ=0, l’équation admet une racine réelle double x1=x2 et S= {x1}. Le trinôme ax2+bx+c se factorise en a(x-x1)2.
3ème cas : Δ<0, l’équation n’a pas des racines réelles et S= { } . Le trinôme ax2+ bx + c ne se factorise pas.