

Synthèse.
On appelle nombre complexe z, tout couple (a, b) des nombres réels.
Tout nombre complexe s’écrit de façon unique z=a + bi, où a est appelé « partie réelle de z » et est notée R(z), b « partie imaginaire de z » et est notée I(z) et i l’unité imaginaire.
On écrit : z= a+bi = R(z)+I(z)i
z=a+bi est donc la forme cartésienne ou algébrique de z.
Remarques
Exemples : z=2 z=-143 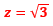
On constate que l’ensemble I des puissances de i est constitué de 4 éléments :I={1, i, -1, -i}
La règle suivante permet de trouver rapidement une puissance ne de i.

D’où : in=i4k+r (r est le reste de la division de n par 4).
Exemples
4. Deux nombres complexes peuvent être additionnés, soustraits, multipliés ou divisés.
Le résultat étant dans tous les cas un nouveau complexe.
Par exemple : pour les nombres complexes z1=a1+ib1 et z2=a2+ib2 ;
z1+z2=(a1+ib1)+ (a2+ib2)
=(a1+a2) + (b1+b2)i
z1-z2=(a1+ib1)-(a2+ib2)
=(a1-a2)+(b1-b2)i
z1 . z2=(a1 + ib1) . (a2+ib2)
=a1 . a2 + (a1 . b2+ a2 . b1) i-b1. b2
(a + ib)2=(a + ib)2(a + ib)2
=(a2-b2)+2abi