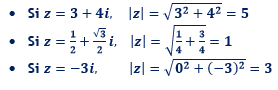Construction de l'ensemble C des nombres complexes (suite 2)

 Synthèse.

4. Calculer la somme, la différence, le produit et le quotient des nombres complexes.

5. Restituer :

1. La définition de l’opposé, du conjugué et de l’inverse d’un nombre complexe ;
2. La définition et la notation du module d’un nombre complexe z.

Division

La division est plus subtile. Pour obtenir un nombre complexe de la forme a+bi à partir d’un rapport 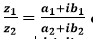 de nombres complexes, on multiplie le numérateur et le dénominateur par le conjugué de l’expression du dénominateur.

D’où :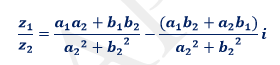 

5. L’opposé d’un nombre complexe z=a+bi  est –z=-a-bi.

Le conjugué d’un nombre complexe z est le nombre complexe noté z et défini par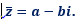 

Exemples

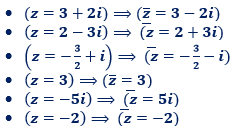
L’inverse d’un nombre complexe non nul z=a + bi est :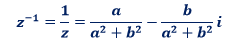 

Soit un nombre complexe z=a + bi. On appelle module de z, le nombre réel positif ou nul noté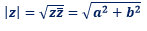  

Exemples