

Rappel
- Effectuez
(a) ( 18x+36y-72z) : 18
(b) (8b-4b) : 4b
Motivation
- Que nous rappellent ces nombres. 0 ; 2 ; 4 ; 6 ; 8 ......
Divise 16 : 2
- Que pouvons-nous dire de 16 par rapport à 2 ?
Annonce du sujet
Aujourd'hui, nous allons étudier
Analyse
- Quand est-ce qu'un nombre a est divisible par un autre nombre b ?
- Comment obtient- on les multiples d'un nombre ?
- Enoncez la définition mathématique de b diviseur de a?
- Comment détermine -t-on les multiples d'un nombre ?
Effectuez
(a) ( 18x+36y-72z) : 18

(b) (8b-4b) : 4b

Les nombres 0,2,4,6,8 .... sont les multiples de 2.
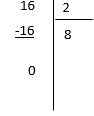
On dit que 16 est divisible par 2 ou 2 divise 16 ou encore 2 est un diviseur de 16.
Aujourd'hui, nous allons étudier LA DIVISIBILITE.
Définition
- Le nombre a est divisible par un autre nombre b s'il existe un entier tel que:
|
a = b . k |
On dit que b est un diviseur de a ou b divise a.
Notation
b divise a se note b/a
Exemple
7 est un diviseur de 21 ou 21 = 7 x 3(k) l'ensemble des diviseurs de 21 est formé de 1,3,7,21.
* a est un multiple de b ssi b est un diviseur de a.
Note : Les multiples d'un nombre s'obtient en multipliant ce nombre par chacun des nombres naturels.
Remarques
* Tout nombre est diviseur de 0
* 1 est diviseur de tout nombre
b/a ↔ a = b .k
- Les multiples d'un nombre sont déterminés en multipliant ce nombre par chacun des nombres naturels.