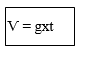Rappel
Un train animé d’une vitesse normale de marche de 72 Km/h, entre en M.R.U.R dont l’accélération retardatrice est de 1m/s2. Après combien de temps le train s’arrêtera – t – il ? quel trajet a – t – il parcouru ?
Motivation
Qu’arrive-t-il à un corps qui est abandonné sur lui – même ?
Annonce du sujet
Qu'est ce que nous allons étudier aujourd'hui ?
Rappel

Motivation
Il tombe sous l’effet de son poids nous dirons qu’il tombe en chute libre.
Annonce du sujet
Aujourd'hui nous allons étudier la chute libre des corps.
Analyse
Qu’est-ce que pesanteur ?
Dans un M.R.U.A partant du repos qu'elle est la formule de l’espace parcouru ?
La vitesse qu’aura un corps au sol est proportionnelle à la durée de la chute ?
Quelle est l formule de la vitesse ?
Analyse
Lorsqu’un corps pesant cesse d’être soutenu, il tombe en chute libre sans l’action de la pesanteur.
Nous pouvons encore les lois qui régissent la chute des corps
1° En absence de l’air, tous les corps tombent de la même manière (expérience du tube de Newton).
2° Le mouvement de chute d’un corps est un mouvement rectiligne uniformément accéléré
En un même endroit du globe terrestre, tous les corps tombent avec la même accélération (loi des accélération)
Donc la terre attiré les corps avec une accélération appelée accélération de la pesanteur g.
g = 9, 8m/s2 ou g = 10 m/s2
3° Les espaces parcourus par un corps qui tombe sont directement proportionnel aux carrés de temps employés à les parcours (li des espaces)

4° Les vitesses acquises par un corps sui tombe sont directement proportionnel à la durée (loi des vitesses)